为了解某社区居民在一次爱心活动中的捐款情况,对该社区部分捐款户的捐款情况进行了调查,并将有关数据整理成如图所示的统计图(不完整).已知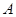 、
、 两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.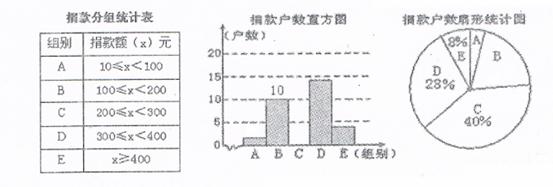
(1)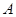 组的频数是 ;本次调查样本的容量 ;
组的频数是 ;本次调查样本的容量 ;
(2)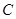 组的频数是 ;
组的频数是 ;
(3)请补全直方图;
(4)若该社区有500户住户,则估计捐款不少于300元的户数 .
某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为多少?
(2)该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
如图①,已知直线y=3x+3与x轴交于点A,与y轴交于点D,与直线y=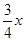 交于点E,
交于点E,
过点D作DC∥x轴,交直线y=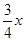 于点C.过点C作CB∥AD交x轴于点B.
于点C.过点C作CB∥AD交x轴于点B.
(1)点C的坐标是 ;
(2)以线段AD的中点M为圆心作⊙M,当⊙M与直线CE相切时,求⊙M的半径;
(3)如图②,点P从点O出发,沿线段OC向终点C运动,点Q从点C出发,沿线段CD向终点D运动.若P、Q两点同时出发,速度均为1单位长度/s,时间为ts,当点Q到达终点时,P、Q两点均停止运动.在点P、Q的运动过程中,将线段PQ绕点P沿顺时针方向旋转90°后,设点Q的对应点为R.当点R落在四边形ABCD一边所在的直线上时,直接写出t的值.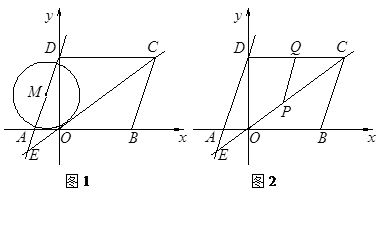
直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=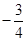 x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.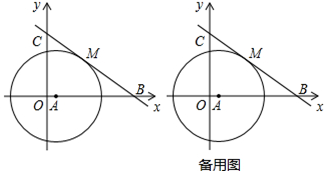
(1)填空:⊙A的半径为 ,b= .(不需写解答过程)
(2)判断直线BC与⊙A的位置关系,并说明理由.
(3)点D是线段OC上的一点,连接MA、MD并延长交⊙A于E、F,若AE⊥AF,求点D的坐标.
一家化工厂原来每月利润为120万元,从今年1月起安装使用回收净化设备(安装时间不计),一方面改善了环境,另一方面大大降低原料成本.据测算,使用回收净化设备后的1至x月(1≤x≤12)的利润的月平均值w(万元)满足w=10x+90,第二年的月利润稳定在第1年的第12个月的水平.
(1)设使用回收净化设备后的1至x月(1≤x≤12)的利润和为y,写出y关于x的函数关系式,并求前几个月的利润和等于700万元;
(2)当x为何值时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等;
(3)求使用回收净化设备后两年的利润总和.
如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π).