计算：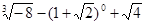
(满分l4分)如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．点P从点C出发沿CA以每秒1个单位长度的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长度的速度向点B匀速运动．伴随着P，Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB—BC—CP于点E．点P，Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P，Q运动的时间是t s(t>O)．
(1)当t=2时，AP=________，点Q到AC的距离是_________；
(2)在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；(不必写出t的取值范围)
(3)在点E从B向C运动的过程中，四边形QBED能否成为直角梯形?若能，请求出t的值；若不能，也请说明理由．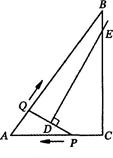
(满分l2分)如图，在梯形ABCD中，AB∥CD，∠A=90°，AB=2，BC=3，CD=1，点E是AD的中点，求证：CE⊥BE．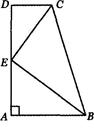
(满分l2分)如图，A，B两城市相距100 km．现计划在这两座城市间修筑一条高速公路(即线段AB)，经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上．已知森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内．请问：计划修筑的这条高速公路会不会穿越保护区?为什么?(参考数据：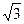
≈1.732，
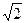≈1.414)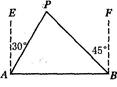
(满分l2分)如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
(1)求证：PB是⊙O的切线；
(2)已知PA=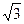
，BC=1，求⊙O的半径．
(满分l0分)2008年北京奥运会后，同学们参与体育锻炼的热情高涨．为了解他们平均每周的锻炼时间，小明同学在校内随机调查了50名同学，统计并制作了如下的频数分布表和扇形统计图(图)．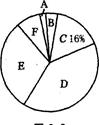
| 组别 |
锻炼时间(时/周) |
频数 |
| A |
1.54≤t<3 |
1 |
| B |
3≤t<4.5 |
2 |
| C |
4.5≤t<6 |
m |
| D |
6≤t<7.5 |
20 |
| E |
7.5≤t<9 |
15 |
| F |
t≥9 |
n |
根据上述信息解答下列问题：
(1)m=_______,n=________；
(2)在扇形统计图中，D组所占圆心角的度数为_________；
(3)全校共有3000名学生，估计该校平均每周体育锻炼时间不少于6h的学生约有多少名?_________。