如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组 的解,点C是直线
的解,点C是直线 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
小云想用7天的时间背诵若干首诗词,背诵计划如下:
①将诗词分成4组,第 组有 首, ,2,3,4;
②对于第 组诗词,第 天背诵第一遍,第 天背诵第二遍,第 天背诵第三遍,三遍后完成背诵,其它天无需背诵, ,2,3,4;
|
第1天 |
第2天 |
第3天 |
第4天 |
第5天 |
第6天 |
第7天 |
|
|
第1组 |
|
|
|
||||
|
第2组 |
|
|
|
||||
|
第3组 |
|||||||
|
第4组 |
|
|
|
③每天最多背诵14首,最少背诵4首.
解答下列问题:
(1)填入 补全上表;
(2)若 , , ,则 的所有可能取值为 ;
(3)7天后,小云背诵的诗词最多为 首.
在平面内,给定不在同一条直线上的点 , , ,如图所示,点 到点 , , 的距离均等于 为常数),到点 的距离等于 的所有点组成图形 , 的平分线交图形 于点 ,连接 , .
(1)求证: ;
(2)过点 作 ,垂足为 ,作 ,垂足为 ,延长 交图形 于点 ,连接 .若 ,求直线 与图形 的公共点个数.

国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
.国家创新指数得分的频数分布直方图(数据分成7组: , , , , , , ;
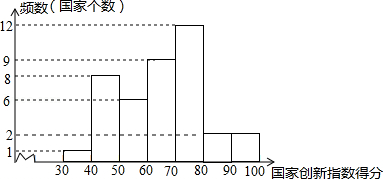
.国家创新指数得分在 这一组的是:
61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
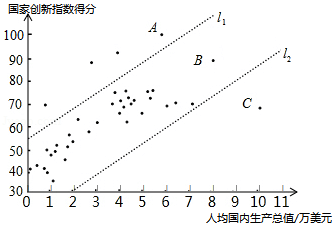
.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告 》
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第 ;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线 的上方,请在图中用“〇”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为 万美元;(结果保留一位小数)
(4)下列推断合理的是 .
①相比于点 , 所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点 , 所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
如图,在菱形 中, 为对角线,点 , 分别在 , 上, ,连接 .
(1)求证: ;
(2)延长 交 的延长线于点 ,连接 交 于点 .若 , ,求 的长.
关于 的方程 有实数根,且 为正整数,求 的值及此时方程的根.