如图,四边形ABCD是矩形, ,
, =90°.
=90°.
(1)求证:AC∥DE.
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
在如图的4×4的方格内画△ABC,使它的顶点都在格点上,使AB=2,BC=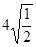 ,AC=
,AC=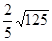 ,并求出最长边上的高。
,并求出最长边上的高。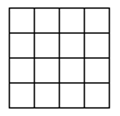
(1)计算:(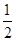 )-2-
)-2-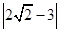 +
+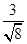 ;
;
(2)先化简,再求值: -
-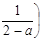 ÷
÷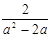 ,其中a是方程x2+3x+1=0的根.
,其中a是方程x2+3x+1=0的根.
阅读理解
如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.
情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;
情形二:如图3,沿 △ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;
将余下的部分沿∠B1A1C的平分线 A1B2折叠,此时点B1与点C重合.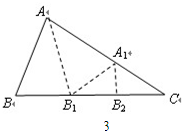
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC (填“是”或“不是”)△ABC的好角;
(2)若经过三次折叠发现∠BAC是△ABC的好角,请探究∠B与∠C之间的等量关系(不妨设∠B>∠C).
根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C之问的等量关系为 .(不妨设∠B>∠C)
应用提升:
(3)小丽找到一个三角形,三个角分别为15º,60º,l05º,发现60º和l05º的两个角都是此三角形的好角.
请你完成,如果一个三角形的最小角是4º,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
如图1,点O是边长为1的等边△ABC内的任一点,设∠AOB=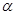 °,∠BOC=
°,∠BOC=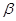 °
°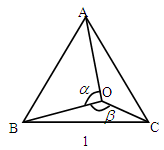
(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。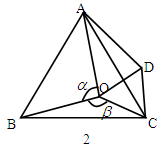
(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE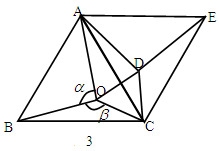
(3)在(2)的基础上, 当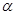 、
、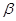 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.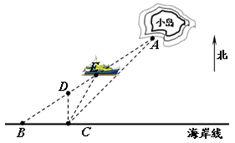
(1)试求出小岛码头A点到海岸线BC的距离;
(2)有一观光客轮K从B至A方向沿直线航行:
①某瞭望员在C处发现,客轮K刚好在正北方向的D处,试求出客轮驶出的距离BD的长;
②当客轮航行至E处时,发现E点在C的北偏东27°处,请求出E点到C点的距离;
(注:tan33°≈0.65,sin33°≈0.54,cos33°≈0.84,结果精确到0.01km)