已知某校5个学生的数学和物理成绩如下表
(1)假设在对这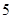 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这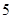 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有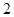 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用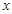 表示数学成绩,用
表示数学成绩,用 表示物理成绩,求
表示物理成绩,求 与
与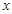 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式: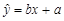 ,其中
,其中 ,
, ;
;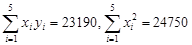 ,残差和公式为:
,残差和公式为:
(本小题共14分)
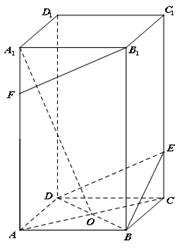
如图,在四棱柱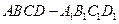 中,底面
中,底面 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点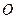 是正方形
是正方形 对角线的交点,
对角线的交点,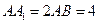 ,点
,点 ,
, 分别在
分别在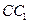 和
和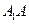 上,且
上,且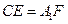 .
.
(Ⅰ)求证: ∥平面
∥平面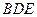 ;
;
(Ⅱ)若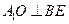 ,求
,求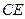 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角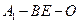 的余弦值.
的余弦值.
(本小题共13分)
某单位在2011新年联欢会上举行一个抽奖活动:甲箱中装有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(本小题共13分)
已知函数 ,且
,且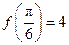 .
.
(Ⅰ)求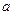 的值;
的值;
(Ⅱ)当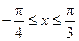 时,求函数
时,求函数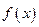 的值域.
的值域.
(本小题14分)已知数列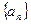 为等差数列,
为等差数列,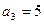 ,
,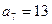 ,数列
,数列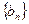 的前
的前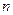 项和为
项和为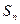 ,且有
,且有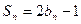
(1)求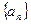 、
、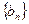 的通项公式;
的通项公式;
(2)若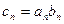 ,
,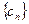 的前
的前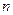 项和为
项和为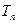 ,求
,求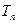 ;
;
(3)试比较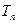 与
与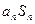 的大小,并说明理由.
的大小,并说明理由.
.(本小题14分)椭圆
 的一个顶点为
的一个顶点为
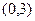 ,离心率
,离心率
(1)求椭圆方程;
(2)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点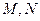 ,且满足
,且满足 ,
, ,求直线
,求直线 的方程.
的方程.