工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别 ,假设
,假设 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为 ,其中
,其中 是
是 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目 的分布列和均值(数字期望)
的分布列和均值(数字期望) ;
;
(Ⅲ)假定 ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm)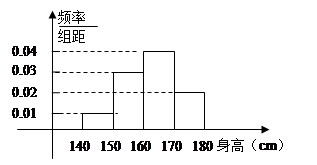
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
(2)在身高为140—160的学生中任选2个,求至少有一人的身高在150—160之间的概率.
设命题 ;命题
;命题 :不等式
:不等式 对任意
对任意 恒成立.若
恒成立.若 为真,且
为真,且 或
或 为真,求
为真,求 的取值范围.
的取值范围.
求经过直线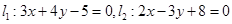 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:
(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.
已知圆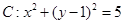 ,直线
,直线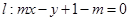 .
.
(1)判断直线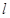 与圆C的位置关系;
与圆C的位置关系;
(2)设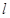 与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
(3)若定点P(1,1)分弦AB为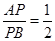 ,求此时直线
,求此时直线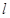 的方程.
的方程.
如图,在平面直角坐标系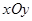 中,点
中,点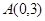 ,直线
,直线 。设圆
。设圆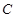 的半径为
的半径为 ,圆心在
,圆心在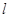 上。
上。
(1)若圆心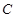 也在直线
也在直线 上,过点
上,过点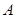 作圆
作圆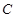 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆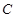 上存在点
上存在点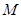 ,使
,使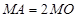 ,求圆心
,求圆心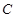 的横坐标
的横坐标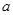 的取值范围。.
的取值范围。.