5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60）
（1）设X为某一时刻需要电力的工人数，求 X的分布列及期望；
（2）如果同一时刻最多能提供3名工人需要的电力，求电力超负荷的概率，并解释实际意义．
如图，某海轮以30海里/小时的速度航行，在点A测得海面上油井P在南偏东60°，向北航行40分钟后到达点B，测得油井P在南偏东30°，海轮改为北偏东60°航向再航行80分钟到达点C，求P、C间的距离。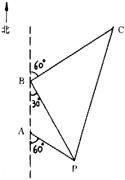
在
中，已知
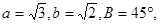求∠A，∠C，边c.
（1）解关于x的不等式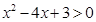
；
（2）若关于x的不等式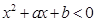
的解集为
，解关于x的不等式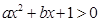
设函数f(x)="|2x-1|+|2x-3|" , x∈R.
(Ⅰ)解不等式f(x)≤5；
(Ⅱ)若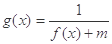
的定义域为R，求实数m的取值范围.
在平面直角坐标系中，直线
的参数方程为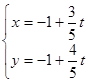
(
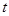为参数）.若以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，则曲线C的极坐标方程为
.
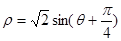(Ⅰ) 求曲线C的直角坐标方程;
(Ⅱ) 求直线被曲线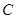
所截得的弦长.