|
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC BD = O,A1C1
BD = O,A1C1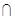 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.
已知函数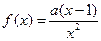 ,其中
,其中 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若直线 是曲线
是曲线 的切线,求实数
的切线,求实数 的值;
的值;
(Ⅲ)设 ,求
,求 在区间
在区间 上的最大值.
上的最大值.
(其中 为自然对数的底数)
为自然对数的底数)
如图,  是边长为
是边长为 的正方形,
的正方形,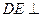 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)设点 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论
,并证明你的结论
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
设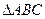 中的内角
中的内角 ,
, ,
, 所对的边长分别为
所对的边长分别为 ,
, ,
, ,且
,且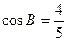 ,
, .
.
(Ⅰ)当 时,求角
时,求角 的度数;(Ⅱ)求
的度数;(Ⅱ)求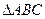 面积的最大值.
面积的最大值.
函数 ,
,
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)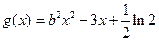 ,当
,当 ,
, 时,
时,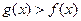 恒有解,求
恒有解,求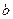 的取值范围.
的取值范围.