先观察下列等式,然后用你发现的规律解答下列问题.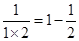 ;
;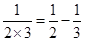 ;
;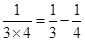 ;┅┅
;┅┅
(1) 计算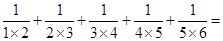 .
.
(2)探究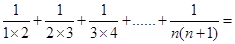 .(用含有
.(用含有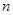 的式子表示)
的式子表示)
(3)若 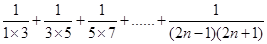 的值为
的值为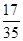 ,求
,求 的值.
的值.
填空或解答:点B、C、E在同一直线上,点A、D在直线CE
的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
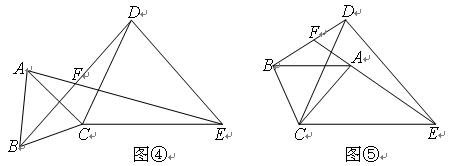
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。
在图④中,∠AFB与∠α的数量关系是________________;
在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。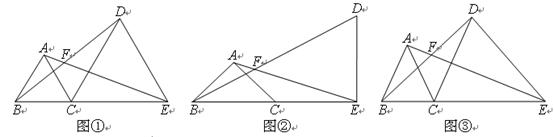
如图,在⊙O中,AB是直径,AD是弦,∠ADE = 60°,∠C = 30°.
(1)判断直线CD是否是⊙O的切线,并说明理由;
(2)若CD = 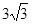 ,求BC的长.
,求BC的长.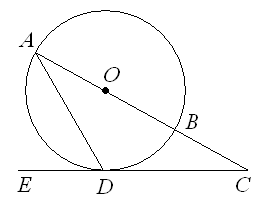
如图,斜坡AC的坡度(坡比)为1: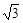 ,AC=10米.坡顶有
,AC=10米.坡顶有
一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.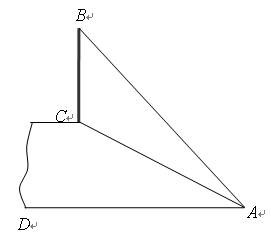
如图,已知一次函数 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式。