(本小题满分12分)
为备战2012奥运会,甲、乙两位射击选手进行了强化训练. 现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3;
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.
(1)画出甲、乙两位选手成绩的茎叶图;(用茎表示成绩的整数部分,用叶表示成绩的小数部分)
(2)现要从中选派一人参加奥运会,从平均成绩和发挥稳定性角度考虑,你认为派哪位选手参加合理? 简单说明理由.
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为 ,求
,求 的分布列及均值E
的分布列及均值E .
.
已知椭圆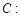
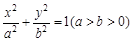 的焦距为
的焦距为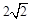 ,且过点
,且过点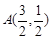 .
.
(1)求椭圆的方程;
(2)已知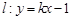 ,是否存在
,是否存在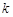 使得点
使得点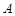 关于
关于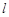 的对称点
的对称点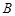 (不同于点
(不同于点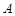 )在椭圆
)在椭圆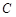 上?若存在求出此时直线
上?若存在求出此时直线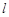 的方程,若不存在说明理由.
的方程,若不存在说明理由.
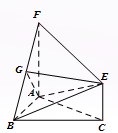
如图,三角形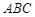 和梯形
和梯形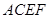 所在的平面互相垂直,
所在的平面互相垂直, 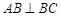 ,
,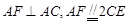 ,
,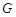 是线段
是线段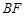 上一点,
上一点,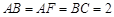 .
.
(Ⅰ)当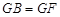 时,求证:
时,求证: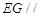 平面
平面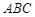 ;
;
(Ⅱ)求二面角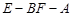 的正弦值;
的正弦值;
(Ⅲ)是否存在点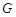 满足
满足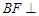 平面
平面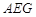 ?并说明理由.
?并说明理由.
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(Ⅰ)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量 的分布列和数学期望.
的分布列和数学期望.
在△ABC中,已知A=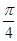 ,
,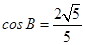 .
.
(Ⅰ)求cosC的值;
(Ⅱ)若BC=2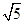 ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长.
(本小题满分10分)选修4-5:不等式选讲
已知函数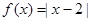 ,
,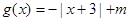 .
.
(1)若关于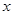 的不等式
的不等式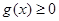 的解集为
的解集为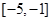 ,求实数
,求实数 的值;
的值;
(2)若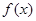 的图象恒在
的图象恒在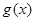 图象的上方,求实数
图象的上方,求实数 的取值范围.
的取值范围.