某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对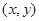 表示“甲在
表示“甲在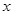 号车站下车,乙在
号车站下车,乙在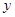 号车站下车”
号车站下车”
(1)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(2)求甲、乙两人同在第3号车站下车的概率;
(3)求甲、乙两人在不同的车站下车的概率.
在直角坐标系 中,以
中,以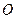 为圆心的圆与直线
为圆心的圆与直线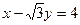 相切.
相切.
(Ⅰ)求圆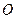 的方程;
的方程;
(Ⅱ)圆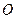 与
与 轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB| 成等比数列,求
轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB| 成等比数列,求 的取值范围.
的取值范围.
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。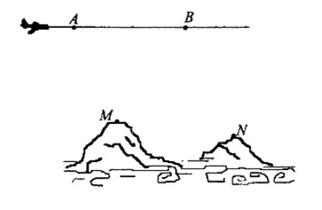
设数列 满足
满足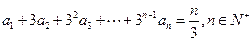 .
.
(I)求数列 的通项;
的通项;
(II)设 ,求数列
,求数列 的前
的前 项和
项和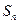 .
.
 的内角
的内角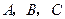 的对边分别为
的对边分别为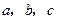 ,且
,且 .
.
(I)求角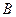 的大小;
的大小;
(II)若 最大边的边长为
最大边的边长为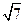 ,且
,且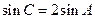 ,求最小边长.
,求最小边长.
已知射线 和点
和点 ,试在
,试在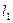 上求一点
上求一点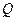 使得
使得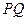 所在直线
所在直线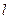 和
和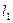 、直线
、直线 在第一象限围成的面积达到最小值,并写出此时直线
在第一象限围成的面积达到最小值,并写出此时直线 的方程。
的方程。