如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
“双十一”淘宝网销售一款工艺品,每件的成本是50元.销售期间发现:销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件.但要求销售单价不得低于成本.设当销售单价为x元时,每天的销售利润为y元.
(1)求出y与x之间的函数表达式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果每天的销售利润不低于4000元,那么每天的总成本至少需要 元.
(每天的总成本=每件的成本×每天的销售量)
如图,在Rt△ABC中,∠ACB=90°,AC=6,D为BC边上一点,CD=3,过A,C,D三点的⊙O与斜边AB交于点E,连结DE.
(1)求证:△BDE ∽△BAC;
(2)求△ACD外接圆的直径的长;
(3)若AD平分∠CAB,求出BD的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°.请把Rt△ABC分割成三个三角形,其中有两个三角形和原Rt△ABC相似,第三个三角形为等腰三角形.画图要求: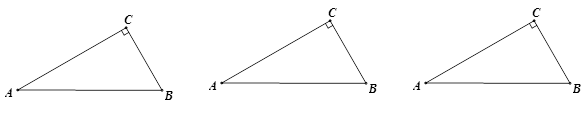
(1)工具不限,画图准确,标出能说明画法的符号或角度.
(2)用三种不同的方法画图,有一条分割线的位置不同即视为不同的画法.
如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.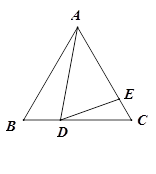
(1)求证:△ABD∽△DCE;
(2)若AB=9cm,BD=3cm,求EC的长.
在不透明的布袋里装有白、红、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球有1个,红球有2个,黄球1个.
(1)求从袋中摸出一个球恰好是黄球的概率;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是红球的概率.