如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
(1)判断DE与⊙O的位置关系并说明理由;(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
 |
解不等式组 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
(1)计算:3(–π)0– + (–1)2011
(2)先化简,再求值: – ,其中x = –3
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG, 求证:AG∥HE
求证:AG∥HE
已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 4,求a的值.
 |
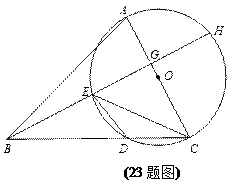
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
 |