已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 4,求a的值.
 |
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
在△ABC中,BC=24cm,外心O到BC的距离为5cm,求△ABC的外接圆半径.
已知Rt△ABC的两直角边为a和b,且a,b是方程x2﹣3x+1=0的两根,求Rt△ABC的外接圆面积.
△ABC在直角坐标系的位置如图所示,按要求解答
(1)将△ABC绕O点旋转180°后得到△A1B1C1,请画出△A1B1C1
(2)在图中画出△ABC的外接圆M,并在图中标出M的坐标.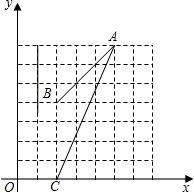
二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,且OA、OB的长是方程x2﹣5x+4=0的两根,且OA>OB,与y轴交于点C(0,4).
(1)求4a﹣2b+c的值;
(2)连接AC、BC,P是线段AB上一动点,且AP=m,过点P作PM∥AC,交BC于M,当m为何值时,S△PCM的面积最大,并求出这个最大值;
(3)△ABC外接圆的面积是.(直接写出答案,结果保留π)