阅读材料:
(1)对于任意两个数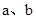 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当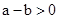 时,一定有
时,一定有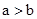 ;
;
当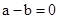 时,一定有
时,一定有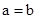 ;
;
当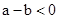 时,一定有
时,一定有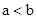 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数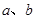 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵ ,
,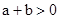
∴(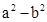 )与(
)与(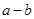 )的符号相同
)的符号相同
当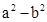 >0时,
>0时,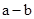 >0,得
>0,得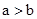
当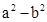 =0时,
=0时,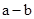 =0,得
=0,得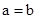
当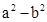 <0时,
<0时,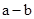 <0,得
<0,得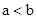
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1= (用x、y的式子表示)
W2= (用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案: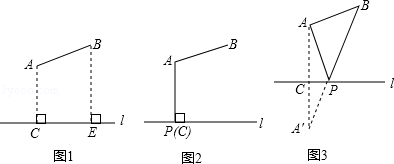
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= km(用含x的式子表示);
②在方案二中,a2= km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费;即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.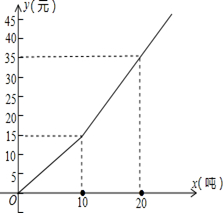
(1)分段写出y与x的函数关系式.
(2)某户居民上月用水8吨,应收水费多少元?
(3)已知居民甲上月比居民乙多用水4吨,两家一共交水费46元,求他们上月分别用水多少吨?
某景点的门票价格规定如下表
| 购票人数 |
1—50人 |
51—100人 |
100人以上 |
| 每人门票价 |
12元 |
10元 |
8元 |
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
如图所示,已知矩形ABCD中,AD=8cm,AB=6cm,对角线AC的垂直平分线交AD于E,交BC于F.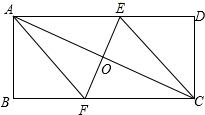
(1)试判断四边形AFCE是怎样的四边形;
(2)求出四边形AFCE的周长.
阅读下列材料:如图(1)在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为“筝形”
解答问题:如图(2)将正方形ABCD绕着点B逆时针旋转一定角度后,得到正方形GBEF,边AD与EF相交于点H.请你判断四边形ABEH是否是“筝形”,说明你的理由.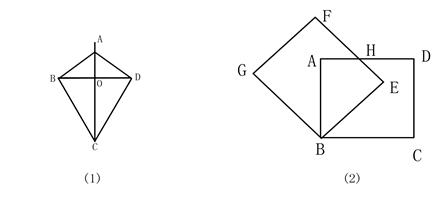
已知点A(2,2),B(-4,2),C(-2,-1),D(4,-1).在如图所示的平面直角坐标系中描出点A、B、C、D,然后依次连结A、B、C、D得到四边形ABCD,试判断四边形ABCD的形状,并说明理由.