如图，AD是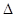
ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，AB=AC.四边形PQRS是正方形。
（1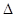）ASR与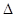ABC相似吗？为什么？
（2）求正方形PQRS的边长。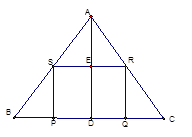
△ABC在直角坐标系中的位置如图所示，直线l经过点（-1，0），并且与y轴平行．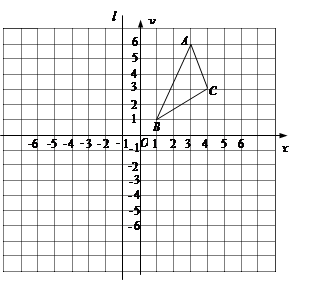
（1）将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1，在图中画出△A1B1C1，并写出△A1B1C1三个顶点的坐标；
（2）△A2B2C2与△ABC关于直线l对称，画出△A2B2C2，并写出△A2B2C2三个顶点的坐标.
解方程(1)
(2)x2－2x－4=0
(3)
(4)2x2―3x―5=0
如图，在平面直角坐标系中，矩形OABC的顶点A在y轴正半轴上，点B的横、纵坐标分别是一元二次方程x2+5x﹣24=0的两个实数根，点D是AB的中点．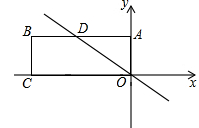
（1）求点B坐标；
（2）求直线OD的函数表达式；
（3）点P是直线OD上的一个动点，当以P、A、D三点为顶点的三角形是等腰三角形时，请直接写出P点的坐标．
（1）已知，如图①，在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE=BD+CE．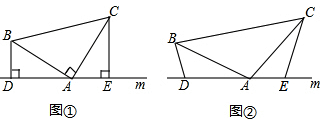
（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意钝角，请问结论DE=BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．
山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：
（1）每千克核桃应降价多少元？
（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？