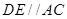山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同,求甲、乙工程队每天各能铺设多少米?
小明去超市买三种商品,其中丙商品单价最贵,如果购买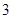 件甲商品、
件甲商品、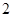 件乙商品和
件乙商品和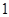 件丙商品,那么需要付费
件丙商品,那么需要付费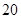 元,如果购
元,如果购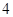 件甲商品、
件甲商品、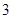 件乙商品和
件乙商品和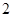 件丙商品,那么需要付费
件丙商品,那么需要付费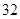 元.
元.
(1)如果购买三种商品各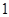 件,那么需要付费多少元?
件,那么需要付费多少元?
(2)如果需要购买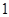 件甲商品、
件甲商品、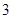 件乙商品和
件乙商品和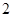 件丙商品,那么小明至少带多少钱才能保证一定能全部买到?(结果精算到元)
件丙商品,那么小明至少带多少钱才能保证一定能全部买到?(结果精算到元)
在平面直角坐标系中,已知点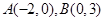 ,
, 为原点
为原点
(1)求三角形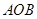 的面积
的面积
(2)若点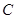 在坐标轴上,且三角形
在坐标轴上,且三角形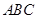 的面积为
的面积为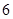 ,求点
,求点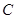 的坐标
的坐标
已知关于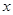 的不等式组
的不等式组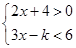
(1)当 为何值时,该不等式组的解集为
为何值时,该不等式组的解集为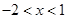
(2)若该不等式组只有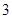 个正整数解,求一个满足条件的整数
个正整数解,求一个满足条件的整数 的值。
的值。
已知:如图,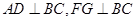 ,垂足分别为
,垂足分别为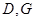 ,且
,且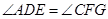
求证: