在平面直角坐标系xOy中，矩形ABCO的顶点A、C分别在y轴、x轴正半轴上，点P在AB上，PA=1，AO=2．经过原点的抛物线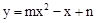
的对称轴是直线x=2．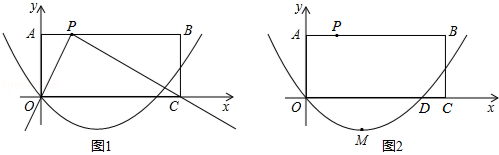
（1）求出该抛物线的解析式．
（2）如图1，将一块两直角边足够长的三角板的直角顶点放在P点处，两直角边恰好分别经过点O和C．现在利用图2进行如下探究：
①将三角板从图1中的位置开始，绕点P顺时针旋转，两直角边分别交OA、OC于点E、F，当点E和点A重合时停止旋转．请你观察、猜想，在这个过程中，
的值是否发生变化？若发生变化，说明理由；若不发生变化，求出的值．
②设（1）中的抛物线与x轴的另一个交点为D，顶点为M，在①的旋转过程中，是否存在点F，使△DMF为等腰三角形？若不存在，请说明理由．
已知：关于x的方程
.求证：方程有两个不相等的实数根；
当
时，方程的两根之和为，两根之积为若方程的一个根是
，求
的值；
解方程：
如图，
是
的外接圆，点
在
上， 
，点
是垂足，
连接
．求证：
是的切线．若
的半径为10cm，∠A=600，求CD的长
计算、解方程：（
－
）－（
－
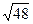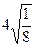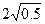）x(2x-5)=4x-10．
水果市场某批发商经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克.现要保证每天盈利6000元，同时又要让顾客尽可能多得到实惠，那么每千克应涨价多少元？
若该批发商单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多.