(本小题满分13分)已知:等差数列{an}中,a1=1,S3=9,其前n项和为Sn.
(1)求数列{an}的通项公式;
(2)设bn=,求数列{bn}的前n项和T
如图所示,在直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上的点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与CD有怎样的位置关系?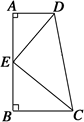
如图所示,AB为⊙O的直径,AE平分∠BAC交⊙O于E点,过E作⊙O的切线交AC于点D,试判断△AED的形状,并说明理由.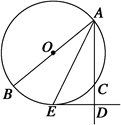
(拓展深化)如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.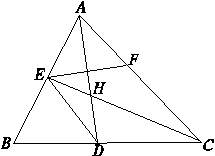
(1)证明:B、D、H、E四点共圆;
(2)证明:CE平分∠DEF.
如图所示,AB、CD都是圆的弦,且AB∥CD,F为圆上一点,延长FD、AB交于点E.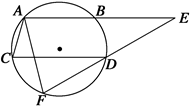
求证:AE·AC=AF·DE.
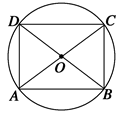
试说明矩形的四个顶点在以对角线的交点为圆心的同一个圆上.