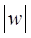已知抛物线
的焦点
也是椭圆
的一个焦点,
与
的公共弦的长为
.
(1)求
的方程;
(2)过点
的直线
与
相交于
两点,与
相交于
两点,且
与
同向
(ⅰ)若
,求直线
的斜率
(ⅱ)设
在点
处的切线与
轴的交点为
,证明:直线
绕点
旋转时,
总是钝角三角形
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为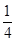 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求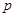 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为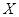 ,求
,求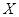 的分布列和数学期望
的分布列和数学期望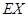 .
.
已知数列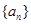 中,
中,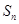 是
是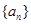 的前
的前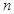 项和,且
项和,且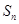 是
是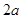 与
与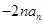 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求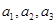 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.
设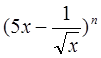 的展开式的各项系数之和为
的展开式的各项系数之和为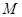 ,二项式系数之和为
,二项式系数之和为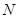 ,
,
若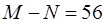 ,(1) 求 n,N,M(2)求展开式中常数项为.
,(1) 求 n,N,M(2)求展开式中常数项为.
用数字0,1,2,3,4,5组成没有重复数字的数.
求:(1)可以组成多少个四位数?
(2)可以组成多少个不同的四位偶数?
(3)可以组成多少个能被5整除的四位数?
已知复数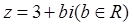 ,且
,且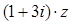 为纯虚数.
为纯虚数.
(1)求复数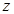 ;(2)若
;(2)若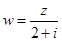 ,求复数
,求复数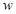 的模
的模