某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球和1个白球的甲箱与装有2个红球和2个白球的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(Ⅰ)用球的标号列出所有可能的摸出结果;
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
已知函数 ,其中
,其中 为大于零的常数,
为大于零的常数,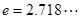 ,函数
,函数 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为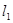 ,函数
,函数 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为 ,且
,且 .
.
(I)若在闭区间 上存在
上存在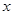 使不等式
使不等式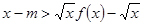 成立,求实数
成立,求实数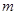 的取值范围;
的取值范围;
(II)对于函数 和
和 公共定义域内的任意实数
公共定义域内的任意实数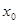 ,我们把
,我们把 的值称为两函数在
的值称为两函数在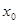 处的偏差.求证:函数
处的偏差.求证:函数 和
和 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
已知椭圆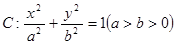 的两个焦点分别为
的两个焦点分别为 ,且
,且 ,点
,点 在椭圆上,且
在椭圆上,且 的周长为6.
的周长为6.
(I)求椭圆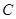 的方程;
的方程;
(II)若点 的坐标为
的坐标为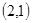 ,不过原点
,不过原点 的直线与椭圆
的直线与椭圆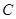 相交于
相交于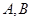 两点,设线段
两点,设线段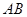 的中点为
的中点为 ,点
,点 到直线的距离为
到直线的距离为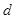 ,且
,且 三点共线.求
三点共线.求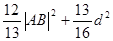 的最大值.
的最大值.
已知函数 ,其中
,其中 为正实数,
为正实数,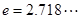 .
.
(I)若 是
是 的一个极值点,求
的一个极值点,求 的值;
的值;
(II)求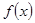 的单调区间.
的单调区间.
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中
随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: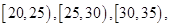
 .
.
(I)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在 岁的人数;
岁的人数;
(II)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
如图,在长方体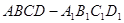 中,
中,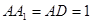 ,
, 为
为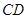 的中点,
的中点,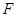 为
为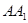 的中点.
的中点.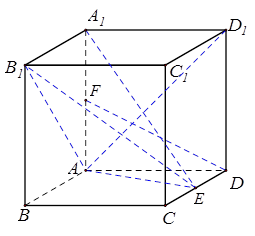
(I)求证: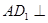 平面
平面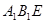 ;
;
(II)求证: 平面
平面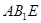 ;
;
(III)若二面角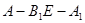 的大小为
的大小为 ,求
,求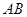 的长.
的长.