如图,已知四边形 为正方形,
为正方形, 平面
平面 ,
, ∥
∥ ,且
,且 .
.
(Ⅰ)求证: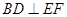 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知数列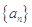 满足
满足 ,
,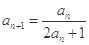 .
.
(Ⅰ)求证: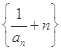 是等差数列;
是等差数列;
(Ⅱ)证明: .
.
(本小题满分10分)选修4—5:不等式选讲
已知函数 ,
,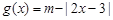 .
.
(Ⅰ)若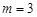 ,解不等式
,解不等式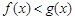 ;
;
(Ⅱ)若不等式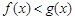 有解,求
有解,求 的取值范围.
的取值范围.
选修4—4坐标系与参数方程
在直角坐标系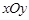 和极坐标系中,极点与原点重合,极轴与
和极坐标系中,极点与原点重合,极轴与 轴非负半轴重合,曲线
轴非负半轴重合,曲线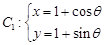 (
(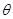 为参数),曲线
为参数),曲线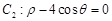 .
.
(Ⅰ)将曲线 方程化为普通方程,将曲线
方程化为普通方程,将曲线 方程化为直角坐标方程;
方程化为直角坐标方程;
(Ⅱ)判断曲线 与曲线
与曲线 的位置关系,若曲线
的位置关系,若曲线 与曲线
与曲线 相交,求公共弦长.
相交,求公共弦长.
选修4—1几何证明选讲
如图所示,在四边形 中,
中, 交
交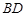 于点
于点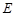 ,
,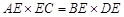 .
.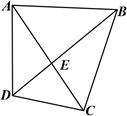
(Ⅰ)求证: 、
、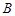 、
、 、
、 四点共圆;
四点共圆;
(Ⅱ)过 作四边形
作四边形 外接圆的切线交
外接圆的切线交 的延长线于
的延长线于 ,
,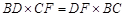 ,求证:
,求证: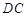 平分
平分 .
.