(本小题满分13分)
已知函数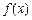 的导数
的导数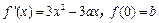 .a,b为实数,
.a,b为实数, .
.
(1)若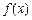 在区间
在区间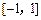 上的最小值、最大值分别为
上的最小值、最大值分别为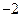 、1,求a、b的值;
、1,求a、b的值;
(2)在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3)设函数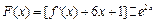 ,试判断函数
,试判断函数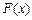 的极值点个数.
的极值点个数.
已知平面 ∥
∥ ,在
,在 内有4个点,在
内有4个点,在 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选.
有6本不同的书按下列分配方式分配,问共有多少种不同的分配方式?
(1)分成1本、2本、3本三组;
(2)分给甲、乙、丙三人,其中一人1本,一人2本,一人3本;
(3)分成每组都是2本的三组;
(4)分给甲、乙、丙三人,每人2本.
用0、1、2、3、4、5这六个数字,可以组成多少个分别符合下列条件的无重复数字的四位数:(1)奇数;(2)偶数;(3)大于3 125的数.
4个不同的球,4个不同的盒子,把球全部放入盒内.
(1)恰有1个盒不放球,共有几种放法?
(2)恰有1个盒内有2个球,共有几种放法?
(3)恰有2个盒不放球,共有几种放法?