某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨。
,已知此生产线年产量最大为210吨。
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求每吨产品平均最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
已知曲线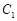 :
: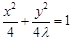 ,曲线
,曲线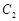 :
: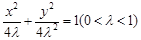 .曲线
.曲线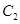 的左顶点恰为曲线
的左顶点恰为曲线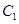 的左焦点.
的左焦点.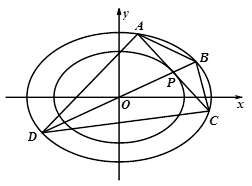
(Ⅰ)求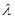 的值;
的值;
(Ⅱ)设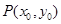 为曲线
为曲线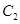 上一点,过点
上一点,过点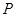 作直线交曲线
作直线交曲线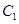 于
于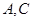 两点. 直线
两点. 直线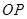 交曲线
交曲线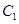 于
于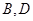 两点. 若
两点. 若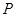 为
为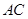 中点,
中点,
① 求证:直线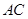 的方程为
的方程为 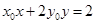 ;
;
② 求四边形 的面积.
的面积.
浑南“万达广场”五一期间举办“万达杯”投掷飞镖比赛.每3人组成一队,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面正方形 如图所示,其中阴影区域的边界曲线近似为函数
如图所示,其中阴影区域的边界曲线近似为函数 的图像).每队有3人“成功”获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
的图像).每队有3人“成功”获一等奖,2人“成功” 获二等奖,1人“成功” 获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
(Ⅰ)求某队员投掷一次“成功”的概率;
(Ⅱ)设 为某队获奖等次,求随机变量
为某队获奖等次,求随机变量 的分布列及其期望.
的分布列及其期望.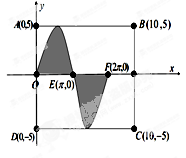
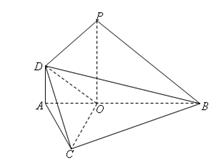
(本小题满分12分)如图,在 中,已知
中,已知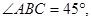
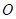 在
在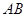 上,且
上,且 又
又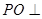 平面
平面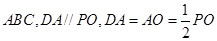 .
.
(Ⅰ)求证: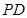 ⊥平面
⊥平面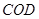 ;
;
(Ⅱ)求二面角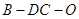 的余弦值.
的余弦值.
(本小题满分12分)在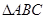 中,内角
中,内角 的对边分别为
的对边分别为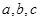 ,已知
,已知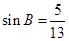 ,且
,且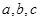 成等比数列.
成等比数列.
(Ⅰ)求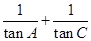 的值;
的值;
(Ⅱ)若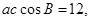 求
求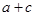 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
设函数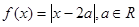 。
。
(Ⅰ)若不等式 的解集为
的解集为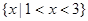 ,求
,求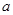 的值;
的值;
(Ⅱ)若存在 ,使
,使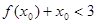 ,求实数a的取值范围。
,求实数a的取值范围。