已知△
的两个顶点
的坐标分别是
，
，且
所在直线的斜率之积等于
．
（1）求顶点
的轨迹
的方程，并判断轨迹为何种圆锥曲线；
（2）当
时，过点
的直线
交曲线
于
两点，设点
关于
轴的对称点为
(
不重合)， 试问：直线
与
轴的交点是否是定点？若是，求出定点，若不是，请说明理由.
设圆C满足：（1）截
轴所得弦长为2；（2）被
轴分成两段圆弧，其弧长的比为5∶1．
在满足条件（1）、（2）的所有圆中，求圆心到直线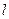
：3－4=0的距离最小的圆的方程．
某集团为了获得更大的收益，每年要投入一定的资金用于广告宣传，经调查，每投入广告费t（百万元）可增加的销售额约为
（百万元）。
（I）若该公司将当年的广告宣传费控制在3百万元之内，则应投入多少广告费才能使公司由此获得的收益最大。
（II）现该公司准备投入3百万元，分别用于广告宣传和技术改造，经预测，每投入技术改造费x（百万元）可增加的销售额约为
（百万元），请设计资金分配方案，使该公司由
此获得的收益最大。（注：收益=销售额—投入）
平面内给定三个向量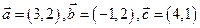
，回答下列问题：
（Ⅰ）求满足
的实数m,n；
（Ⅱ）若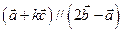
，求实数k；
(本小题满分10分)
有一根钢管，长度是4000mm，要截成500mm和600mm两种毛坯，且这两种数量比大于
配套，问怎样截取所得毛坯总数最多？
(本小题满分12分)
设各项均为正数的数列
的前n项和为
，已知
，数列
是公差为
的等差数列。
（1）求数列的通项公式（用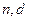
表示）；
（2）设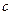
为实数，对满足
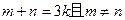的任意正整数
，不等式
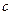都成立。求证：的最大值为
。