抛物线 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ,若椭圆
,若椭圆 以
以 、
、 为焦点、
为焦点、
且离心率为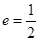 。
。
(1)当 时求椭圆
时求椭圆 的方程;
的方程;
(2)若抛物线 与直线
与直线
 及
及 轴所围成的图形的面积为
轴所围成的图形的面积为 ,求抛物线
,求抛物线 和直线
和直线 的方程
的方程
 某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
某工厂生产甲、乙两种产品,每种产品都是经过第一和第二工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级.对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品.
(1)已知甲、乙两种产品每一道工序的加工结
果为A级的概率如表一所示,分别求生产
出的甲、乙产品为一等品的概率P甲、P乙;
(2)已知一件产品的利润如表二所示,用ξ、 η分别表示一件甲、乙产品的利润,在
η分别表示一件甲、乙产品的利润,在
(I)的条件下,求ξ、η的分布列及
Eξ、Eη;
(3)已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名,可用资.
|
金60万元.设x、y分别表示生产甲、乙产
|
 品的数量,在(II)的条件下,x、y为何
品的数量,在(II)的条件下,x、y为何
 最大?最大值是多少?
最大?最大值是多少?
6本不同的书,按照以下要求处理,各有几种分法?
(1)一堆一本,一堆两本,一堆3本;(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得两本,一人得三本;(4)平均分给甲、乙、丙三人;(5)平均分成三堆。
甲、乙两门高射炮同时向一敌机开炮,已知甲击中敌机的概率为0.6,乙击中敌机的概率为0.8,求敌机被击中的概率(用两种方法求解).
50件产品中有3件次品,不放回地抽取2次,每次抽1件,已知第1次抽出的是次品,求第2次抽出的也是次品的概率.
为防止某突发事件,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后突发事件不发生的概率(记为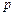 )和所需费如下表:
)和所需费如下表:
| 预防措施 |
甲 |
乙 |
丙 |
丁 |
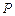 |
0.9 |
0.8 |
0.7 |
0.6 |
| 费用(万元) |
90 |
60 |
30 |
10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施.在总费不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.