设不等式 确定的平面区域为
确定的平面区域为 ,
,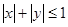 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取
内任取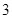 个整点,求这些整点中恰有
个整点,求这些整点中恰有 个整点在区域
个整点在区域 内的概率;
内的概率;
(2)在区域 内任取
内任取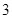 个点,记这
个点,记这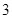 个点在区域
个点在区域 内的个数为
内的个数为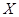 ,求
,求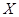 的分布列,数学期望
的分布列,数学期望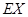 及方差
及方差 .
.
(本小题满分12分)已知函数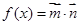 ,其中
,其中 ,
, 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)在

 的面积.
的面积.
(本小题满分12分)已知 是三角形
是三角形 三内角,向量
三内角,向量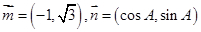 ,且
,且
(1)求角 ;(2)若
;(2)若 ,求
,求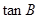 。
。
(本小题满分12分)已知y=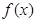 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求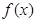 的解析式;
的解析式;
(2)求函数 的单调递减区间及值域..
的单调递减区间及值域..
(本小题满分12分)在锐角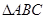 中,角
中,角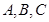 所对边分别为
所对边分别为 ,已知
,已知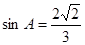 .
.
(Ⅰ)求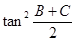 的值;
的值;
(Ⅱ)若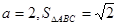 ,求
,求 的值.
的值.
(I) 已知抛物线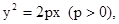 过焦点
过焦点 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;
(Ⅱ)由 (Ⅰ) 可知: 过抛物线的焦点 的动直线 l 交抛物线于
的动直线 l 交抛物线于 两点, 存在定点
两点, 存在定点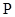 ,使得
,使得 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.