行驶中的汽车，在刹车后由于惯性的作用，要继续向前滑行一段距离后才会停下，这段距离叫刹车距离。为测定某种型号汽车的刹车性能，对这种型号的汽车在国道公路上进行测试，测试所得数据如下表。根据表中的数据作散点图，模拟函数可以选用二次函数或函数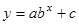
（其中
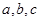为常数）．某人用（0,0），（10,1.1），（30,6.9）求出相关系数，用（60,24.8）验证，请问用以上哪个函数作为模拟函数较好，并说明理由．在一次由这种型号的汽车发生的交通事故中，测得刹车距离为14.4m，问汽车在刹车时的速度大概是多少？
（其中用函数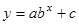拟合，经运算得到函数式为
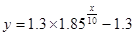，且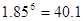
）
| 刹车时车速v/km/h |
10 |
15 |
30 |
50 |
60 |
80 |
|||
| 刹车距离s/m |
1.1 |
2.1 |
6.9 |
17.5 |
24.8 |
42.5 |
|
||
，
，
为
的三内角，其对边分别为
，
，
，若
．
，求
中，
，其通项公式为
，前
项和为
；
，试求数列
的前
；
，试求数列
的前
；
中，内角
所对边的边长分别是
，若
，∠A＝105°，求c边长。
；
的前
项和为
，已知
，
．
和公比
的值；
，求