(本小题满分14分)
如图所示,已知圆 ,
, 为定点,
为定点, 为圆
为圆 上的动点,线段
上的动点,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,点
,点 的轨迹为曲线E.
的轨迹为曲线E.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)过点 作直线
作直线 交曲线
交曲线 于
于 两点,设线段
两点,设线段 的中垂线交
的中垂线交 轴于点
轴于点 ,求实数m的取值范围.
,求实数m的取值范围.
(本小题满分12分)
如图 ,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD =90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.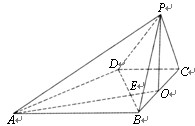
(1)求证:PA⊥BD;
(2)求二面角P—DC—B的 大小;
大小;
(本小题满分12分)
某学校为提升数字化信息水平,在校园之间架设了7条网线,这7条网线其中有两条能通过一个信息量,有三条能通过两个信息量,有两条能通过三个信息量.现从中任选三条网线,设可通 过的信息量为X,当可通过的信息量不小于6时,则可保证校园内的信息通畅.
过的信息量为X,当可通过的信息量不小于6时,则可保证校园内的信息通畅.
(1)求线路信息通畅的概率;
(2)求线路可通过的信息量X的分布列和数学期望.
(本小题满分12分)
已知△ABC中,角A,B,C对边分别是a,b,c,且tanB=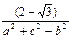 ,
,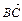 ·
· .
.
(1)求tanB的值;
(2)求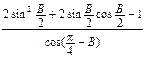 的值.
的值.
((本小题满分14分)
已知两点M(-1,0),N(1,0),且点P使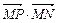 ,
, ,
,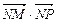 成公差小于零的等差数列。
成公差小于零的等差数列。
(1)点P的轨迹是什么曲线?
(2)若点P的坐标为(x0,y0),记为θ为 的夹角,求tanθ.
的夹角,求tanθ.
((本小题满分13分)
已知a>0,函数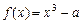 ,x∈[0,+∞).设x1>0,记曲线
,x∈[0,+∞).设x1>0,记曲线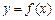 在点M(x1,
在点M(x1,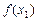 )处的切线为l.
)处的切线为l.
(1)求l的方程;
(2)设l与x轴的交点为(x2,0).证明:
①x2 ;②若x1
;②若x1 ,则
,则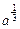 <x2<x1.
<x2<x1.