已知某类型的高射炮在它们控制的区域内击中具有某种速度敌机的概率为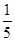 .
.
(Ⅰ)假定有5门这种高射炮控制某个区域,求敌机进入这个区域后被击中的概率;
(Ⅱ)要使敌机一旦进入这个区域内有90%以上的概率被击中,至少需要布置几门这类高射炮?(参考数据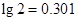 ,
,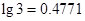 )
)
在公差为
的等差数列
中,已知
,且
,
,
成等比数列.
(Ⅰ)求
,
;
(Ⅱ)若
,求
.
在锐角
中,内角
的对边分别为
,且
.
(Ⅰ)求角A的大小;
(Ⅱ)若
,求
的面积.
已知函数
.
(1)求
的反函数的图象上图象上,点(1,0)处的切线方程;
(2)证明: 曲线
与曲线
有唯一公共点.
(3)设
, 比较
与
的大小, 并说明理由.
已知动点
到直线
的距离是它到点
的距离的2倍.
(1)求动点
的轨迹
的方程;
(2)过点
的直线
与轨迹
交于
两点.若
是
的中点,求直线
的斜率.
有7位歌手(1至7号)参加一场歌唱比赛, 由500名大众评委现场投票决定歌手名次, 根据年龄将大众评委分为5组, 各组的人数如下:
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
(1)为了调查评委对7位歌手的支持状况, 现用分层抽样方法从各组中抽取若干评委, 其中从B组中抽取了6人. 请将其余各组抽取的人数填入下表.
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
| 抽取人数 |
6 |
(2)在(1)中, 若A, B两组被抽到的评委中各有2人支持1号歌手, 现从这两组被抽到的评委中分别任选1人, 求这2人都支持1号歌手的概率.