一名工人要看管三台机床，在一小时内机床不需要工人照顾的概率对于第一台是0.9，第二台是0.8，第三台是0.85，求在一小时的过程中不需要工人照顾的机床的台数X的数学期望(均值)．
已知函数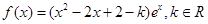
。
（1）求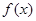
的单调区间；
（2）若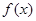在区间
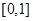上的最小值为e，求k的值。
某商场预计从2013年1月份起的前x个月，顾客对某商品的需求总量p（x）（单位：件）与x的关系近似的满足
，且
）。该商品第x月的进货单价q（x）（单位：元）与x的近似关系是
（1）写出这种商品2013年第x月的需求量f（x）（单位：件）与x的函数关系式；
（2）该商品每件的售价为185元，若不计其他费用且每月都能满足市场需求，试问该商场2013年第几个月销售该商品的月利润最大，最大月利润为多少元？
已知函数
。
（1）当
时，求曲线
在
处切线的斜率；
（2）求
的单调区间；
（3）当
时，求在区间
上的最小值。
已知一次函数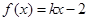
满足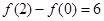
。
（1）求
的解析式；
（2）求函数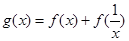
的值域。
已知数列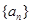
是公差为－2的等差数列，
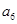是
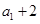与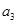
的等比中项。
（1）求数列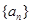的通项公式；
（2）设数列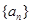的前n项和为
，求的最大值。