(本小题满分16分)某仓库为了保持库内温度,四周墙上装有如图所示的通风设施,该设施的下部是等边三角形ABC,其中AB=2米,上部是半圆,点E为AB的中点.△EMN是通风窗,(其余部分不通风)MN是可以沿设施的边框上下滑动且保持与AB平行的伸缩杆(MN和AB不重合).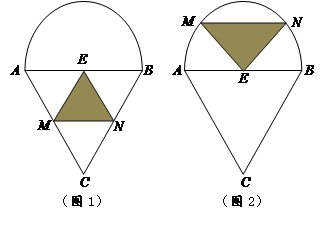
(1)设MN与C之间的距离为x米,试将△EMN的面积S表示成 的函数
的函数 ;
;
(2)当MN与C之间的距离为多少时,△EMN面积最大?并求出最大值.
(本小题满分12分)
如图,P是正三角形ABC所在平面外一点,M、N分别是AB和PC的中点,且PA=PB=PC=AB=a。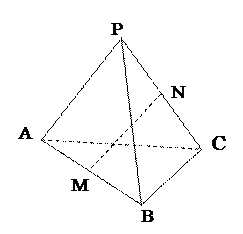
(1)求证:MN是AB和PC的公垂线
(2)求异面直线AB和PC之间的距离
(本小题满分10分)
已知向量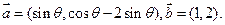
(1)若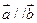 ,求
,求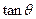 的值;
的值;
(2)若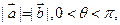 求
求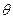 的值。
的值。
((本题16分)
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.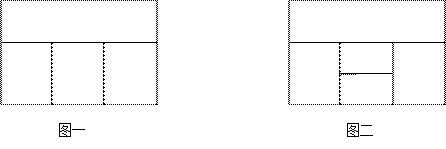
①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
((本题16分)
已知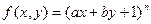 (常数
(常数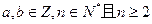 )
)
(1)若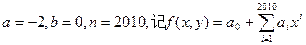 求:①
求:①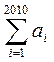 ;②
;②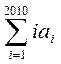
(2)若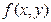 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
((本题15分)
两个人射击,甲射击一次中靶概率是 ,乙射击一次中靶概率是
,乙射击一次中靶概率是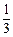 ,
,
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(3)两人各射击5次,是否有99%的把握断定他们至少中靶一次?