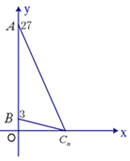
(本小题满分12分)如图,定点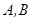 的坐标分别为
的坐标分别为 ,一质点
,一质点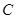 从原点出发,始终沿
从原点出发,始终沿 轴的正方向运动,已知第1分钟内,质点
轴的正方向运动,已知第1分钟内,质点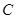 运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第
运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第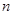 分钟内质点运动了
分钟内质点运动了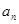 个单位,此时质点的位置为
个单位,此时质点的位置为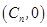 .
.
(Ⅰ)求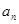 、
、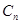 的表达式;
的表达式;
(Ⅱ)当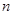 为何值时,
为何值时,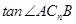 取得最大,最大值为多少?
取得最大,最大值为多少?
( 本题满分13分)
本题满分13分)
如图,点A、B分别是椭圆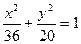 长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
长轴的左、右端点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴的上方,PA⊥PF.
(1)求点P的坐标;
(2)设M椭圆长轴AB上的一点,M到直线AP的距离等于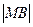 ,求椭圆上的点到点M的距离d的最小值
,求椭圆上的点到点M的距离d的最小值
已知 数列
数列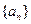 中,
中,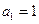 ,
,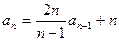
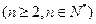 .且
.且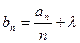 k为等比数列。
k为等比数列。
(Ⅰ) 求实数 及数列
及数列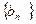 、
、 的通项公式;
的通项公式;
(Ⅱ) 若 为
为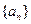 的前
的前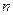 项和,求
项和,求
已知函数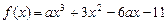 ,
,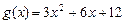 ,和直线
,和直线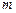 :
: .
.
又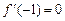 .
.
(1)求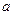 的值;
的值;
(2)是否存在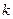 的值,使直线
的值,使直线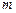 既是曲线
既是曲线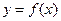 的切线,又是
的切线,又是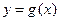 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有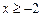 的
的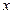 ,都有
,都有 成立,求k的取值范围.
成立,求k的取值范围.
已知椭圆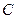 :
: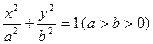 的离心率为
的离心率为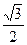 ,过坐标原点
,过坐标原点 且斜率为
且斜率为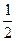 的直线
的直线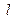 与
与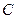 相交于
相交于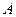 、
、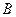 ,
,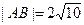 .
.
⑴求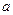 、
、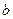 的值;
的值;
⑵若动圆 与椭圆
与椭圆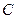 和直线
和直线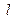 都没有公共点,试求
都没有公共点,试求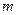 的取值范围.
的取值范围.
(
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为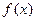 ,
,
求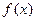 的最大值;
的最大值;

(3)当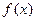 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.