已知点(1, 2)在函数 (
(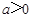 且
且 )的图象上,等比数列
)的图象上,等比数列 的前
的前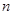 项和为
项和为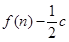 ,数列
,数列
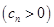 的首项为c,且其前
的首项为c,且其前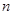 项和
项和 满足 2
满足 2 =
= .
.
(1)求数列 和
和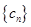 的通项公式;
的通项公式;
(2)若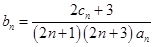 ,求数列
,求数列 的前
的前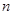 项和
项和 .
.
(本小题满分15分)
在数列 中,
中, ,
, 为
为 的前
的前 项和,且
项和,且
(1)比较 与
与 大小;
大小;
(2)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
(本小题满分15分)
已知 是椭圆
是椭圆 的左、右顶点,
的左、右顶点, ,过椭圆
,过椭圆 的右焦点
的右焦点 的直线交椭圆于点
的直线交椭圆于点 ,交直线
,交直线 于点
于点 ,且直线
,且直线 的斜率成等差数列,
的斜率成等差数列, 和
和 是椭圆上的两动点,
是椭圆上的两动点, 和
和 的横坐标之和为2,
的横坐标之和为2, (不垂直
(不垂直 轴)的中垂线交
轴)的中垂线交 轴与于
轴与于 点.
点.
(1)求椭圆 的方程;
的方程;
(2)求 的面积的最大值
的面积的最大值
(本小题满分15分)
已知二次函数 满足条件:
满足条件:
①当 时,
时, ,且
,且 ;
;
②当 时,
时, ;
;
③ 在R上的最小值为0
在R上的最小值为0
(1)求 的解析式;
的解析式;
(2)求最大的m(m>1),使得存在 ,只要
,只要 ,就有
,就有 .
.
(本小题满分15分)
如图(1)所示,直角梯形 中,
中, ,
, ,
, ,
, .过
.过 作
作 于
于 ,
, 是线段
是线段 上的一个动点.将
上的一个动点.将 沿
沿 向上折起,使平面
向上折起,使平面 平面
平面 .连结
.连结 ,
, ,
, (如图(2)).
(如图(2)).
(Ⅰ)取线段 的中点
的中点 ,问:是否存在点
,问:是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的长;不存在,说明理由;
的长;不存在,说明理由;
(Ⅱ)当 时,求平面
时,求平面 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分14分)
设△ABC的内角A、B、C所对的边长分别为A、B、C,且 成等差数列
成等差数列
(1)求角A的值;
(2)若 ,求
,求 的面积.
的面积.