（本小题满分12分）某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人.，陈老师采用两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果，期末考试后，陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率直方图（如下图）.记成绩不低于90分者为“成绩优秀”.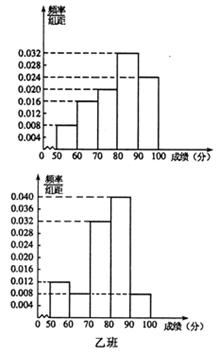 
（I）从乙班随机抽取2名学生的成绩，记“成绩优秀”的人数为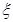
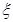，求的分布列和数学期望；
（II）根据频率分布直方图填写下面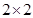
列联表，并判断是否有
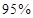的把握认为：“成绩优秀”与教学方式有关.
（本小题共13分）
某校高三年级有男生105人，女生126人，教师42人，用分层抽样的方法从中抽取13人，进行问卷调查.设其中某项问题的选择支为“同意”，“不同意”两种，且每人都做了一种选择.下面表格中提供了被调查人答卷情况的部分信息.
| 同意 |
不同意 |
合计 |
|
| 教师 |
1 |
||
| 女生 |
4 |
||
| 男生 |
2 |
（I）请完成此统计表；
（II）试估计高三年级学生“同意”的人数；
（III）从被调查的女生中选取2人进行访谈，求选到的两名学生中，恰有一人“同意”一人“不同决的概率.”
（本小题共13分）
如图，在四棱锥P—ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，∠ABC=
∠BAD=90°，AD＞BC，E，F分别为棱AB，PC的中点.
（I）求证：PE⊥BC；
（II）求证：EF//平面PAD.
（本小题共13分）
已知函数
（I）当a=1时，求函数
的最小正周期及图象的对称轴方程式；
（II）当a=2时，在
的条件下，求
的值.
（本小题共14分）
已知数列
满足
，点
在直线
上.
（I）求数列的通项公式；
（II）若数列
满足
求
的值；
（III）对于（II）中的数列，求证：
（本小题共14分）
已知椭圆
的离心率为
（I）若原点到直线
的距离为
求椭圆的方程；
（II）设过椭圆的右焦点且倾斜角为
的直线
和椭圆交于A，B两点.
（i）当
，求b的值；
（ii）对于椭圆上任一点M，若
，求实数
满足的关系式.