在极坐标系中,直线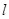 的方程为
的方程为 ,在直角坐标系
,在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为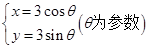 .
.
(Ⅰ)判断直线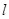 与圆
与圆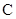 的位置关系;
的位置关系;
(Ⅱ)设点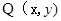 是曲线
是曲线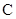 上的一个动点,若不等式
上的一个动点,若不等式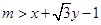 有解,求
有解,求 的取值范围.
的取值范围.
(本小题共12分)已知O为坐标原点,椭圆 的短轴长为2,F为其右焦点,P为椭圆上一点,且PF与x轴垂直,
的短轴长为2,F为其右焦点,P为椭圆上一点,且PF与x轴垂直, 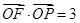 .
.
(1)求椭圆C的方程;
(2)直线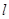 与椭圆C交于不同的两点A、B,若以AB为直径的圆恒过原点O,求
与椭圆C交于不同的两点A、B,若以AB为直径的圆恒过原点O,求 弦长的最大值.
弦长的最大值.
(本小题共12分)已知函数 (k为常数,
(k为常数,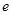 =2.71828是自然对数的底数).函数
=2.71828是自然对数的底数).函数 的导函数为
的导函数为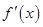 ,且
,且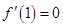 .
.
(1)求k的值;
(2)设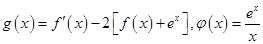 ,
,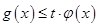 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围.
(本小题共12分)已知E是矩形ABCD(如图1)边CD上的一点,现沿AE将△DAE折起至△D1AE(如图2),并且平面D1AE⊥平面ABCE,图3为四棱锥D1—ABCE的主视图与左视图.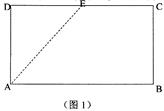
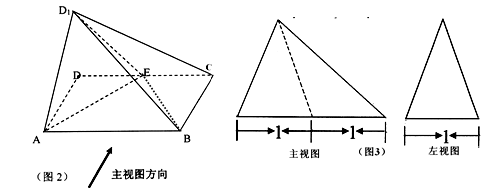
(1)求证:直线BE⊥平面D1AE;
(2)求点A到平面D1BC的距离.
(本小题共12分)甲、乙两位同学玩猜数字游戏:
(1)给出四个数字0,1,2,5,先由甲将这四个数字组成一个四位数,然后由乙来猜甲的四位数是多少,求乙猜对的概率;
(2)甲先从1,2,3,4,5,6这六个数中任选出两个数(不考虑先后顺序),然后由乙来猜.若乙至少答对一个数则乙赢,否则甲赢.问这种游戏规则公平吗?请说明理由.
(本小题共12分)对于数列 ,定义其积数是
,定义其积数是 .
.
(1)若数列 的积数是
的积数是 ,求
,求 ;
;
(2)等比数列 中,
中,
 的等差中项,若数列
的等差中项,若数列 的积数
的积数 满足
满足 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.