(本小题共12分)甲、乙两位同学玩猜数字游戏:
(1)给出四个数字0,1,2,5,先由甲将这四个数字组成一个四位数,然后由乙来猜甲的四位数是多少,求乙猜对的概率;
(2)甲先从1,2,3,4,5,6这六个数中任选出两个数(不考虑先后顺序),然后由乙来猜.若乙至少答对一个数则乙赢,否则甲赢.问这种游戏规则公平吗?请说明理由.
已知函数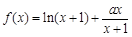
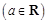 .
.
(Ⅰ)当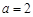 时,求函数
时,求函数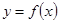 的图象在
的图象在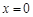 处的切线方程;
处的切线方程;
(Ⅱ)判断函数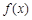 的单调性;
的单调性;
(Ⅲ)求证: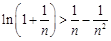 (
(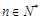 ).
).
如图,圆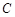 与
与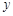 轴相切于点
轴相切于点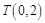 ,与
,与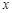 轴正半轴相交于两点
轴正半轴相交于两点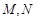 (点
(点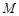 在点
在点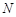 的左侧),且
的左侧),且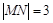 .
.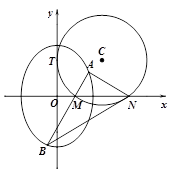
(Ⅰ)求圆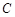 的方程;
的方程;
(Ⅱ)过点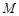 任作一条直线与椭圆
任作一条直线与椭圆 相交于两点
相交于两点 ,连接
,连接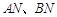 ,求证:
,求证: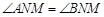 .
.
如图,三棱柱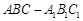 中,
中,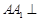 平面
平面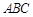 ,
, ,
,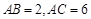 , 点
, 点 在线段
在线段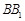 上,且
上,且 ,
,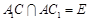 .
.
(Ⅰ)求证:直线 与平面
与平面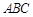 不平行;
不平行;
(Ⅱ)设平面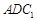 与平面
与平面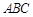 所成的锐二面角为
所成的锐二面角为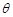 ,若
,若 ,求
,求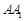 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面 ,求直线
,求直线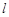 与
与 所成的角的余弦值.
所成的角的余弦值.
招聘会上,某公司决定先试用后再聘用小强,该公司的甲、乙两个部门各有4个不同岗位.
(Ⅰ)公司随机安排小强在这两个部门中的3个岗位上进行试用,求小强试用的3个岗位中恰有2个在甲部门的概率;
(Ⅱ)经试用,甲、乙两个部门都愿意聘用他.据估计,小强可能获得的岗位月工资及相应概率如下表所示:
甲部门不同岗位月工资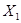 (元) (元) |
2200 |
2400 |
2600 |
2800 |
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
乙部门不同岗位月工资 (元) (元) |
2000 |
2400 |
2800 |
3200 |
获得相应岗位的概率 |
0.4 |
0.3 |
0.2 |
0.1 |
求甲、乙两部门月岗位工资的期望与方差,据此请帮助小强选择一个部门,并说明理由.
若圆C过点M(0,1)且与直线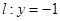 相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点
相切,设圆心C的轨迹为曲线E,A、B(A在y轴的右侧)为曲线E上的两点,点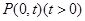 ,且满足
,且满足
(Ⅰ)求曲线E的方程;
(Ⅱ)若t=6,直线AB的斜率为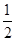 ,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;
(Ⅲ)分别过A、B作曲线E的切线,两条切线交于点 ,若点
,若点 恰好在直线
恰好在直线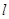 上,求证:t与
上,求证:t与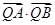 均为定值.
均为定值.