如图,三棱柱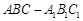 中,
中,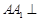 平面
平面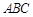 ,
, ,
,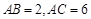 , 点
, 点 在线段
在线段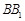 上,且
上,且 ,
,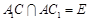 .
.
(Ⅰ)求证:直线 与平面
与平面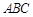 不平行;
不平行;
(Ⅱ)设平面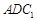 与平面
与平面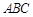 所成的锐二面角为
所成的锐二面角为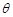 ,若
,若 ,求
,求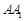 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面 ,求直线
,求直线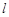 与
与 所成的角的余弦值.
所成的角的余弦值.
求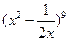 展开式的:
展开式的:
(1)第6项的二项式系数;
(2)第3项的系数;
(3) 的系数
的系数
为调查某重点中学的学生是否需要心理辅导,用简单随机抽样的方法从该学校各年级调查了500名学生,结果如下:
| 男 |
女 |
|
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该学校全体学生中,需要心理辅导的学生的比例;
(2)能否有99%的把握认为该学校的学生是否需要心理辅导与性别有关?
附1: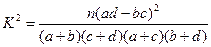
附2:
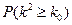 |
0.050 |
0.010 |
0.001 |
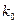 |
3.841 |
6.635 |
10.828 |
(本小题满分14分)
已知函数
(Ⅰ)若函数 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(Ⅱ)当t 1时,不等式
1时,不等式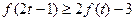 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分14分)
已知数列 满足如图所示的程序框图.(Ⅰ)写出数列
满足如图所示的程序框图.(Ⅰ)写出数列 的一个递推关系式;
的一个递推关系式;
(Ⅱ)证明: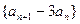 是等比数列,并求
是等比数列,并求 的通项公式;(Ⅲ)求数列
的通项公式;(Ⅲ)求数列 的前
的前 项和
项和 .
.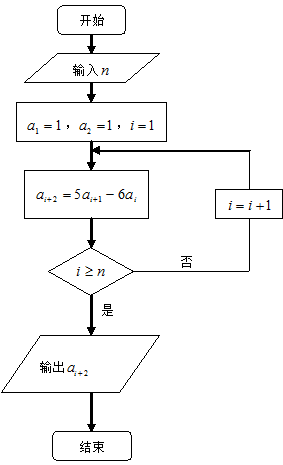
(本小题满分14分)
某商场以100元/件的价格购进一批衬衣,以高于进货价的价格出售,销售期有淡季与旺季之分,通过市场调查发现:
①销售量 (件)与衬衣标价
(件)与衬衣标价 (元/件)在销售旺季近似地符合函数关系:
(元/件)在销售旺季近似地符合函数关系: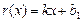 ,在销售淡季近似地符合函数关系:
,在销售淡季近似地符合函数关系: ,其中
,其中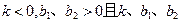 为常数;
为常数;
②在销售旺季,商场以140元/件的价格销售能获得最大销售利润;
③若称①中 时的标价
时的标价 为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
为衬衣的“临界价格”,则销售旺季的“临界价格”是销售淡季的“临界价格”的1.5倍.
请根据上述信息,完成下面问题:
(Ⅰ)填出表格中空格的内容:
 数量关系 数量关系销售关系 |
标价(元/件) |
销售量 (件)(含 (件)(含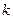 、 、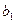 或 或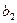 ) ) |
销售总利润 (元)与标价 (元)与标价 (元/件)的函数关系式 |
| 旺季 |
 |
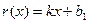 |
|
| 淡季 |
 |
(Ⅱ)在销售淡季,该商场要获得最大销售利润,衬衣的标价应定为多少元/件?