某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100].
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.
| 分数段 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
| x∶y |
1∶1 |
2∶1 |
3∶4 |
4∶5 |
已知函数f(x)＝
x3＋ax2＋bx(a，b∈R)．
(1)当a＝1时，求函数f(x)的单调区间；
(2)若f(1)＝，且函数f(x)在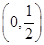
上不存在极值点，求a的取值范围．
已知函数f(x)＝cos
＋2sin2x，x∈R.
(1)求函数f(x)的最小正周期及对称轴方程；
(2)当x∈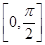
时，求函数f(x)的最大值和最小值及相应的x值．
已知函数f(x)＝sin(ωx＋φ)(ω>0，|φ|<π)的部分图像如图所示，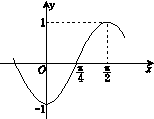
(1)求ω，φ的值；
(2)设g(x)＝2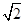
f
f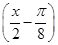
－1，当x∈[0，
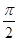]时，求函数g(x)的值域．
已知函数f(x)＝
.
(1)求函数f(x)的定义域；
(2)设α是第四象限的角，且tan α＝－
，求f(α)的值．
在△ABC中，内角A，B，C所对的边分别为a，b，c，cos B＝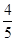
.
(1)求cos(A＋C)的值；
(2)求sin
的值；
(3)若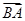
·
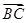＝20，求△ABC的面积．