（本题10分）如图一边长为48cm的正方形铁皮，四角各截去一个大小相同的小正方形，然后折起，可以做成一个无盖长方体容器。所得容器的体积V（单位：
)是关于截去的小正方形的边长x(单位：
)的函数。⑴ 随着x的变化，容积V是如何变化的？
⑵ 截去的小正方形的边长为多少时，容器的容积最大？最大容积是多少？
（1）求动点P的轨迹C的方程；
（2）设M、N是直线l上的两个点，点E是点F关于原点的对称点，若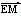
·
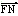＝0，
求 | MN | 的最小值。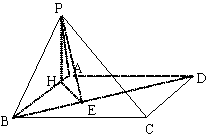
（1）a的值；
（2）函数y＝f (x) 的单调区间；
工作，办公室里只有一部电话机，设经该机打进的电话是打给甲、乙、丙的概率依次为
、
、
。若在一段时间内打进三个电话，且各个电话相互独立。
求：（1）这三个电话是打给同一个人的概率。
（2）这三个电话中恰有两个是打给甲的概率。
AD＝2，PA＝2，PD＝2
，∠PAB＝60°。
（1）证明：AD⊥平面PAB；
（2）求异面直线PC与AD所成的角的大小；
（3）求二面角P－BD－A的大小。
、已知数列 
的前n项和Sn＝2n2+2n数列 
的前 n 项和 Tn＝2－bn
（1）求数列 与 的通项公式；
（2）设Cn＝an2·bn，证明当且仅当n≥3时，Cn+1＜Cn