(本小题满分12分)函数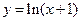
(1)若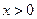 ,证明
,证明 ;
;
(2)若不等式 时
时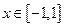 和
和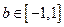 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)已知函数 ,将
,将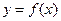 的图象向左平移两个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图象向左平移两个单位,再将图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数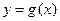 的图象,
的图象,
(1)求函数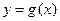 ;(2)求函数
;(2)求函数 的最大值。
的最大值。
(本小题满分12分)关于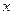 的不等式
的不等式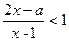 的解集为P, 不等式
的解集为P, 不等式 的解集为Q,若P
的解集为Q,若P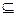 Q,求实数
Q,求实数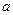 的取值范围。
的取值范围。
若定义在R上的函数 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当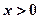 时,
时,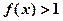 。
。
(1)求证: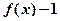 为奇函数;
为奇函数;
(2)求证: 是R上的增函数;
是R上的增函数;
(3)设集合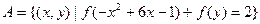 ,
, ,且
,且 , 求实数
, 求实数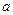 的取值范围。
的取值范围。
(本题12分)若二次函数满足 。
。
(1) 求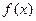 的解析式;
的解析式;
(2) 若在区间[-1,1]上不等式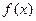 >2x+m恒成立,求实数m的取值范围。
>2x+m恒成立,求实数m的取值范围。