某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为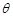 (弧度).
(弧度).
(1)求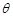 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
设n∈N*,f(n)=1+ +
+ +…+
+…+ ,试比较f(n)与
,试比较f(n)与 的大小.
的大小.
已知f(x)=ax+ (a>1).
(a>1).
(1)证明f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.
ABCD为直角梯形,∠BCD=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若PC与CD不垂直,求证:PA≠PD.
若实数x、y、m满足|x-m|>|y-m|,则称x比y远离m.
(1)若x2-1比1远离0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab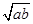 .
.
已知下列三个方程:x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0,其中至少有一个方程有实根,求实数a的取值范围.