(本小题满分12分)已知函数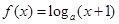 ,
,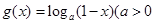 ,且
,且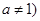
(1)求函数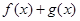 定义域
定义域
(2)判断函数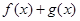 的奇偶性,并说明理由.
的奇偶性,并说明理由.
已知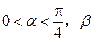 为
为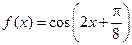 的最小正周期,向量
的最小正周期,向量 ,且a•b
,且a•b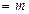 (m为实常数) .求
(m为实常数) .求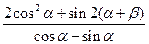 的值.
的值.
(本小题满分14分)
设函数 ,函数y=f(x)-x有唯一的零点,其中实数a为常数,
,函数y=f(x)-x有唯一的零点,其中实数a为常数,
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)求 的值;
的值;
(Ⅲ)若 且
且 ,求证:
,求证: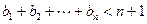 .
.
(本小题满分13分)
已知A、B、C是椭圆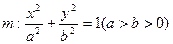 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线L(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且
的直线L(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且 ,求实数t的取值范围.
,求实数t的取值范围.
(本小题满分12分)
已知向量 ,O是坐标原点,动点P满足:
,O是坐标原点,动点P满足:
(Ⅰ)求动点P的轨迹;
(Ⅱ)设B、C是点P的轨迹上不同两点,满足 ,在x轴上是否存在点A(m,0),使得
,在x轴上是否存在点A(m,0),使得 ,若存在,求出实数m的取值范围;若不存在,说明理由。
,若存在,求出实数m的取值范围;若不存在,说明理由。
本小题满分12分)
已知数列 的前
的前 项和
项和 满足
满足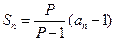
 为常数,且
为常数,且 ,数列
,数列 是等比数列,且
是等比数列,且 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)求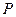 的值。
的值。