2011年夏季，河南小麦喜获丰收，现有甲种小麦1530吨，乙种小麦1150吨，需安排A、B两种不同规格的货厢50节把小麦全部运往上海.已知用一节A型货厢的运费是0.5万元，用一节B型货厢的运费是0.8万元.
（1）设运输这批小麦的总运费为y (万元)，用A型货箱的节数为x (节)，试写出y与x之间的函数关系式；
（2）已知甲种小麦35吨和乙种小麦15吨，可装满一节A型货厢；甲种小麦25吨和乙种小麦35吨可装满一节B型货厢，按此要求安排A、B两种货厢的节数，有哪几种运输方案？请你设计出来.
（3）利用函数的性质说明，在这些方案中，哪种方案总运费最少？最少运费是多少万元？
如图，已知A（0，4），点B在第三象限，且∠B=300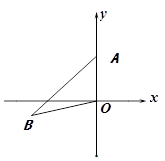
（1）尺规作图：作出△ABO的外接圆⊙P（不写作法，保留作图痕迹）
（2）求点P的坐标．
已知关于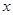
的方程
，
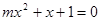（1）当该方程有一根为1时，试确定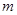
的值
（2）当该方程有两个不相等的实数根时，试确定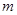的取值范围
先化简，再求值：
，其中
满足x2-2x-4=0
解方程：
（1）4x2－2x－1="0"
（2）
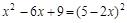
如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC的方向向点C匀速运动，速度为2cm/s，连接PQ，设运动的时间为t（s），其中0＜t＜2，解答下列问题：
（1）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，线段PQ将△ABC的面积分成1：2两部分？若存在，求出此时的t，若不存在，请说明理由；
（3）点P、Q在运动的过程中，△CPQ能否成为等腰三角形？若能，请求出此时t的值，若不存在，请说明理由．