已知：在矩形AOBC中，OB＝4，OA＝3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点（不与B、C重合），过F点的反比例函数
（k＞0）的图象与AC边交于点E.
（1）求证：△AOE与△BOF的面积相等.
（2）记S＝S△OEF－S△ECF，求当k为何值时，S有最大值，最大值为多少？
（3）请探索：是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，请直接写出点F的坐标，若不存在，请说明理由.
（宜宾）如图，某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造．供水站M在笔直公路AD上，测得供水站M在小区A的南偏东60°方向，在小区B的西南方向，小区A、B之间的距离为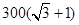
米，求供水站M分别到小区A、B的距离．（结果可保留根号）
（遂宁）计算：
．
（遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：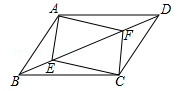
（1）AE=CF；
（2）四边形AECF是平行四边形．
（遂宁）一数学兴趣小组为了测量河对岸树AB的高，在河岸边选择一点C，从C处测得树梢A的仰角为45°，沿BC方向后退10米到点D，再次测得A的仰角为30°，求树高．（结果精确到0.1米，参考数据：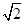
≈1.414，
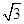≈1.732）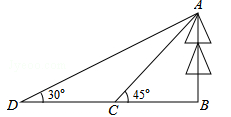
（遂宁）如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．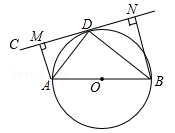
（1）求证：∠ADC=∠ABD；
（2）求证：AD2=AM•AB；
（3）若AM=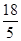
，sin∠ABD=
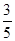，求线段BN的长．