(宜宾)如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为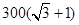 米,求供水站M分别到小区A、B的距离.(结果可保留根号)
米,求供水站M分别到小区A、B的距离.(结果可保留根号)
试解答下列问题:(2+2+4+2=10分)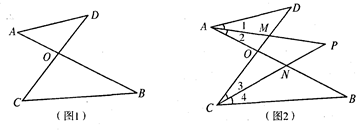
(1)在图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系:;
(2)仔细观察,在图2中“8字形”的个数是个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系.
如图所示,潜望镜的两个镜子是平行放置的,光线经过镜子反射后,有∠1=∠3,∠4=∠6,请你解释为什么进入潜望镜的光线和离开潜望镜的光线也是平行的?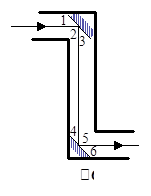
如图,已知MN⊥AB于P,MN⊥CD于Q,∠2=80°,求∠1.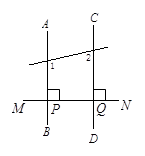
(本题6分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将 △ABC平移,使点A移动到点A′,点B′,点C′分别是B、C的对应点.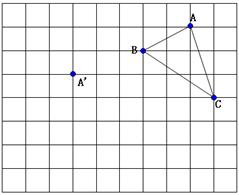
(1)请画出平移后的△A′B′C′;
(2)△A′B′C′的面积是 ;
(3)若连接AA′、CC′,则这两条线段之间的关系是________ ______.
在矩形ABCD中,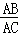 =a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.如图1,当DH=DA时,
=a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.如图1,当DH=DA时,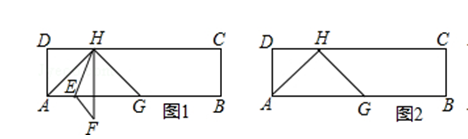
(1)填空:∠HGA=度;
(2)若EF∥HG,求∠AHE的度数,并求此时a的最小值;