(1997•西宁)已知二次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0,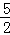 ),(1,6)三点,直线l的解析式为y=2x﹣3
),(1,6)三点,直线l的解析式为y=2x﹣3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
如图所示,要在20米宽,32米长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田,要使花田面积为570m2,则道路应修多宽?
已知关于x的方程mx2﹣(m+2)x+2=0(m≠0).
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
解方程:
(1)x2﹣8x+1=0
(2)3x(x﹣2)=2(2﹣x)
(3)x2+2x﹣3=0.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.
(1)求抛物线的解析式;
(2)点P从O点出发,在线段OB上以每秒1个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动,其中一个点到达终点时,另一点也停止运动,问运动多少秒时,△PBQ的面积最大?最大面积是多少?
(3)过点P向x轴作垂线,交抛物线于一点M,是否存在点M,使得点M到BC的距离等于 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.