(本小题满分14分)
若函数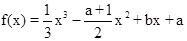 (a,b∈R),且其导函数f′ (x)的图象过原点.
(a,b∈R),且其导函数f′ (x)的图象过原点.
(Ⅰ)当a=1时,求函数f(x)的图象在x=3处的切线方程;
(Ⅱ)若存在x<0使得f′ (x)=-9,求实数a的最大值.
(本小题满分12分)
如图,直三棱柱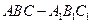 的底面
的底面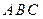 位于平行四边形
位于平行四边形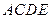 中,
中,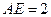 ,
,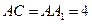 ,
,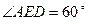 ,点
,点 为
为 中点.
中点.
(1)求证:平面 平面
平面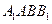 .
.
(2)设二 面角
面角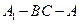 的大小为
的大小为 ,直线
,直线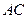 与平面
与平面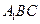 所成的角为
所成的角为 ,求
,求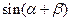 的值.
的值.
(本小题满分12分)
已知实数列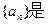 等比数列,其中
等比数列,其中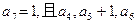 成等差数列.
成等差数列. 
(Ⅰ)求数列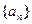 的通项公式;
的通项公式;
(Ⅱ)数列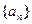 的前
的前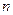 项和记为
项和记为 证明:
证明: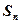 <128
<128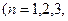 …).
…).
(本小题满分12分 )
)
甲 、乙两名跳高运动员一次试跳
、乙两名跳高运动员一次试跳 米高度成功的概率分别是
米高度成功的概率分别是 ,
,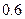 ,且每次试跳成功与否相互之间没有影响,求:
,且每次试跳成功与否相互之间没有影响,求:
(Ⅰ)甲试跳三次,第三次才成功的概率 ;
;
(Ⅱ)甲、乙两人在第一次试跳中至少有一人成功的概率;
(Ⅲ)甲、乙各试跳两次,甲比乙的成功次数恰好多一次的概率.
(本小题 满分10分)
满分10分)
在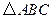 中,
中,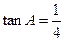 ,
, .
.
(Ⅰ)求角
 的大小;
的大小;
(Ⅱ)若 边的长为
边的长为 ,求
,求 边的长.
边的长.
、(本题满分12分)
定义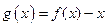 的零点
的零点 为
为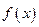 的不动点.已知函数
的不动点.已知函数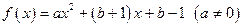
⑴ 当 时,求函数
时,求函数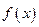 的不动点;
的不动点;
⑵ 对于任意实数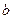 ,函数
,函数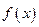 恒有两个相异的不动点,求
恒有两个相异的不动点,求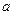
 的取值范围;
的取值范围;
⑶ 若函数 有不变号零点,且
有不变号零点,且 ,求实数
,求实数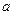 的最小值.
的最小值.