将一根长为16 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为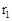 和
和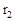 .
.
(1)求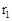 与
与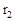 的关系式,并写出
的关系式,并写出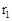 的取值范围;
的取值范围;
(2)将两圆的面积和S表示成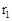 的函数关系式,求S的最小值.
的函数关系式,求S的最小值.
已知点 为正方形 的边 上一点,连接 ,过点 作 ,垂足为 ,交 于点 .
(1)求证: ;
(2)若 为 的中点,求 .

将一副三角板 与 (其中 , , , 如图摆放, 中 所对直角边与 斜边恰好重合.以 为直径的圆经过点 ,且与 交于点 ,分别连接 , .
(1)求证: 平分 ;
(2)求 的值.

在 中, 是 边上的一点,连接 .将 沿 翻折,使点 落在点 处,当 时,求证:四边形 是菱形.

已知 ,以 为直径的 分别交 于 , 于 ,连接 ,若 .
(1)求证: ;
(2)若 , ,求 的长.

如图,四边形 内接于 , , ,垂足为 ,点 在 的延长线上,且 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的值.
