如图，在平面直角坐标系中，直角梯形OABC的边OC、OA分别与x轴、y轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，BC=12
，点C的坐标为（－18，0）。
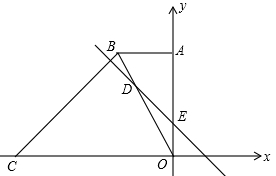
（1）求点B的坐标；
（2）若直线DE交梯形对角线BO于点D，交y轴于点E，且OE=4，OD=2BD，求直线DE的解析式；
（3）若点P是（2）中直线DE上的一个动点，在坐标平面内是否存在点Q，使以O、E、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由。
a与b互为相反数，c与d互为倒数，求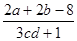
的值。
如图，在△ABC中，∠BAC＝120°，AB＝AC，点D在BC上，且BD＝BA，点E在BC的延长线上，且CE＝CA．
（1）试求∠DAE的度数．
（2）如果把题中“AB＝AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗？请说明理由．
（3）若∠BAC＝α°，其它条件与（2）相同，则∠DAE的度数是多少？为什么？
如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E．
（1）若BC＝10，则△ADE周长是多少？为什么？
（2）若∠BAC＝128°，则∠DAE的度数是多少？为什么？
如图，等腰梯形ABCD中，AB//CD，AD=BC，CE⊥AB于E，AE=DE，AF⊥DE于F，请你判断线段AF与图中的哪条线段相等，先写出你的猜想，再说明理由．
如图，在△ABC中，AB=25，BC=14，BC边上的中线AD=24，
求线段AC的长．